前提知識

サイドフォース
一般にカーブを曲がっている車両においてタイヤの向いている方向とそのタイヤの速度ベクトルの方向は異なる。したがってタイヤ進行方向と垂直方向にはタイヤが横滑りしているような状況となり、地面からの摩擦力を受け、この力のことを「サイドフォース（横力）」と呼ぶ。このサイドフォースをタイヤ速度と垂直方向に射影したものを「コーナリングフォース」と呼ぶ。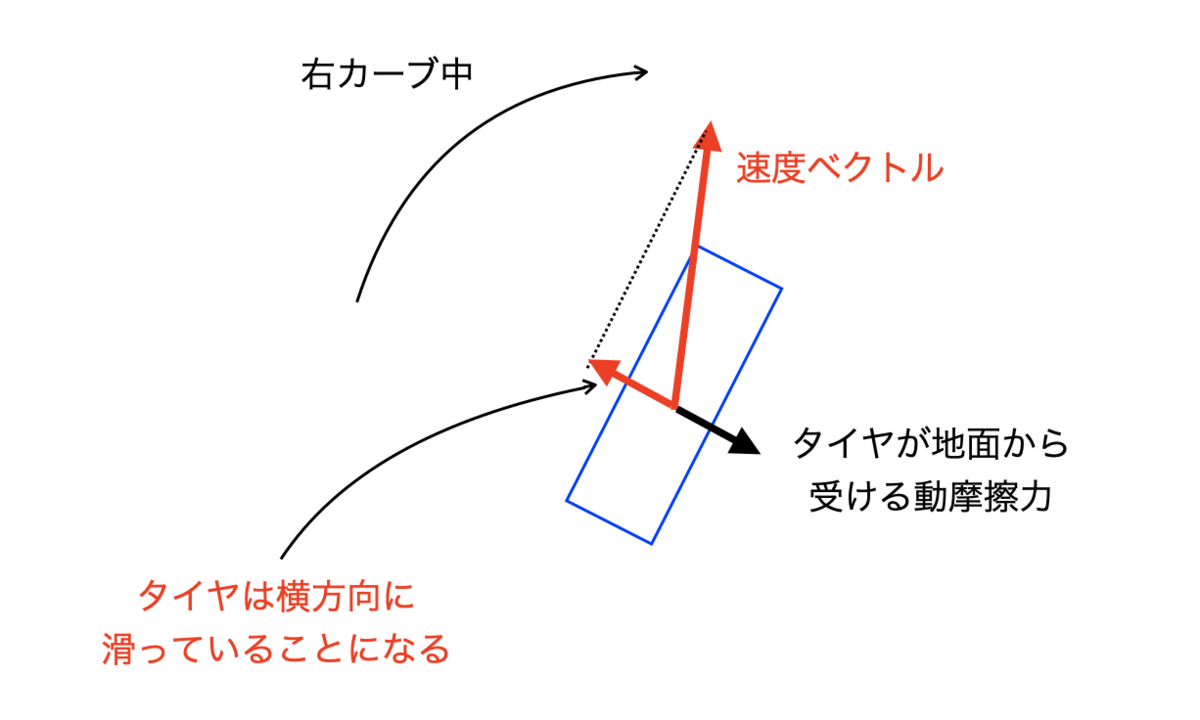
右カーブ中のタイヤに働く摩擦力
旋回中の各タイヤにおける速度ベクトル
カーブを旋回中の車両の前後のタイヤがもつ速度ベクトルの方向は異なる（もし前後のタイヤの速度ベクトルの方向が同じであれば車両は並進移動をするのみで旋回することができない）。後輪が車両中央に到達するまでに $\frac{l_{r}}{v}$ の時間がかかるので、車両が角速度 $\omega$ で回転しているとすると、この間に車両は $\frac{l_{r}\omega}{v}$ だけ速度ベクトルの方向を変えていると近似できる。前輪角についても同様の考察を行えば、

$\begin{eqnarray} \delta - \beta_{f} &=& \beta + \frac{l_{f}}{v}\omega \\ \beta_{r} + \beta &=& \frac{l_{r}}{v}\omega \end{eqnarray}$

と表される。

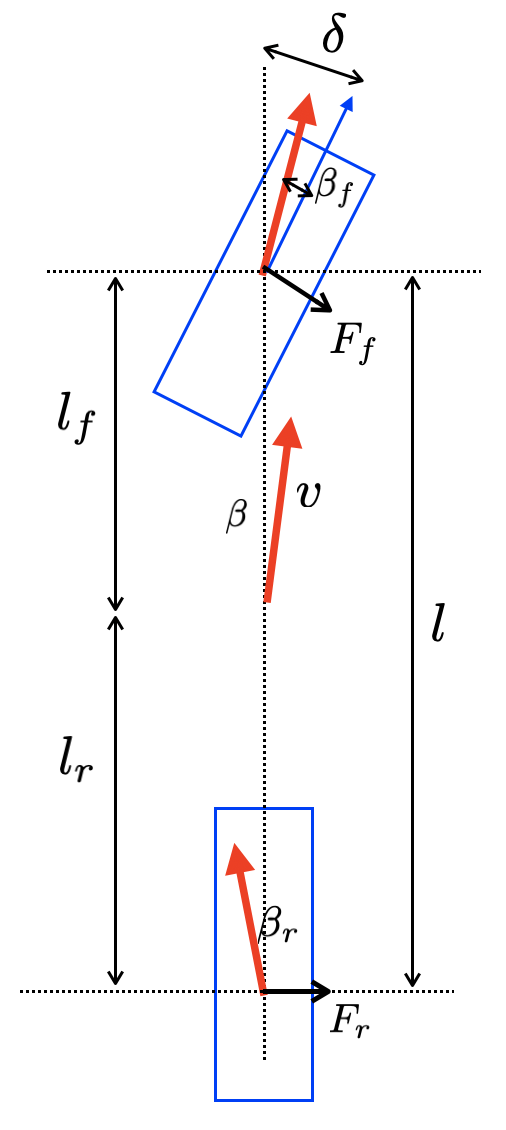
f:id:salpik:20201226170448p:plain:w180 — 右旋回中のタイヤにはたらく力や速度ベクトルを図示したもの。変数は全て符号無しで絶対値で表現している。

コーナリングパワーの導入スリップ角が小さい時はサイドフォースとスリップアングルが比例関係にある。この係数Kをコーナリングパワーと呼ぶ。すなわち

$\begin{eqnarray} F_{f} &=& 2K_{f} \beta_{f} \\ F_{r} &=& 2K_{r} \beta_{r} \end{eqnarray}$

コーナリングパワーが大きいほど、同じスリップアングルでも大きな摩擦力を発揮できる。このパラメータはタイヤの種類にもちろん依存するが、それだけでなく車両の荷重分布にも依存する。それは動摩擦力が垂直抗力に依存するからである。

車両運動方程式

横方向の並進運動方程式およびヨー角に関する回転方程式が基本の方程式となる。

並進運動方程式

後輪方向（図2の点線）と垂直方向に関する運動方程式を考える。車両全体の横速度は $v\sin\beta$ なので、これを微分したものが加速度成分の１つである。また、後輪方向の速度 $v\cos\beta$ が角速度 $\omega$ で回転しており、 $\Delta t$ 時間が経過するとこのベクトルが $\omega \Delta t$ 回転するので $v\sin\omega \Delta t \sim v\omega \Delta t$ の横成分を持つようになるため、横速度変化への寄与として $v\omega \cos\beta$ が加わる。まとめると

$\begin{eqnarray} m\left[ \frac{d}{dt} (v\sin\beta) + v\omega \cos \beta\right] &=& F_{f}\cos\delta + F_{r} \\ m\left[ v\dot{\beta} + v\omega\right] &=& F_{f}\cos\delta + F_{r} \ \ \ \ \ (速度変化はない、すなわち\dot{v}=0と仮定) \end{eqnarray}$

回転運動方程式

慣性モーメントを $I$ 、トルクを $T$ として、 $I\dot{\omega} = T$ であるから

$\begin{equation} I \dot{\omega} = F_{f}l_{f}\cos\delta - F_{r}l_{r} \end{equation}$

定常円の小角度旋回の解

一定の曲率の円を旋回している場合、 $\dot{\beta} = 0$ 、 $\dot{\omega} = 0$ である。また、小角度の旋回であるとして $\beta_{f}, \beta, \beta_{r}, \delta \ll 1$ と仮定する。このとき2つの運動方程式は

$\begin{eqnarray} mv\omega &=& F_{f} + F_{r} \\ 0 &=& F_{f}l_{f} - F_{r}l_{r} \end{eqnarray}$

となる。コーナリングパワーを導入し、2つの式を $\beta$ 、 $\omega$ で表すと

$\begin{eqnarray} mv\omega &=& 2K_{f}\left[ \delta - (\beta + \frac{l_{f}}{v}\omega)\right] + 2K_{r}(-\beta + \frac{l_{r}}{v}\omega) \\ K_{f}\left[ \delta - (\beta + \frac{l_{f}}{v}\omega)\right]l_{f} &=& K_{r}(-\beta + \frac{l_{r}}{v}\omega)l_{r} \end{eqnarray}$

$K_{f}$ と $K_{r}$ の塊があるので、それについてまとめると

$\begin{eqnarray} K_{f}\left[ \delta - (\beta + \frac{l_{f}}{v}\omega)\right] &=& \frac{mv\omega l_{r}}{2(l_{f}+l_{r})} \\\ K_{r}(-\beta + \frac{l_{r}}{v}\omega) &=& \frac{mv\omega l_{f}}{2(l_{f}+l_{r})} \end{eqnarray}$

$K$ を落として両辺を引くと

$\begin{eqnarray} \delta - \frac{l}{v}\omega &=& \frac{mv(K_{r}l_{r}-K_{f}l_{f})}{2K_{f}K_{r}l}\omega \\ \delta &=& \left( \frac{l}{v} + \frac{mv(K_{r}l_{r}-K_{f}l_{f})}{2K_{f}K_{r}l} \right) \omega \\ \omega &=& \frac{\frac{v}{l}\delta}{\frac{l}{v}+\frac{mv(K_{r}l_{r}-K_{f}l_{f})}{2K_{f}K_{r}l}} \\ &=& \frac{1}{1+\frac{m(K_{r}l_{r}-K_{f}l_{f})}{2l^{2}K_{f}K_{r}}v^{2}} \frac{v}{l} \delta \\ \beta &=& \left( \frac{l_{r}}{v} + \frac{mvl_{f}}{2K_{r}l}\right) \\ &=& \frac{\frac{l_{r}}{v}+\frac{mvl_{f}}{2K_{r}l}}{1+\frac{m(K_{r}l_{r}-K_{r}l_{r})}{2l^{2}K_{f}K_{r}}v^{2}} \frac{v}{l}\delta \\ &=& \frac{l_{r} + \frac{ml_{f}}{2K_{r}l}v^{2}}{1+\frac{m(K_{r}l_{r}-K_{r}l_{r})}{2l^{2}K_{f}K_{r}}v^{2}} \frac{\delta}{l}\delta \end{eqnarray}$